머신러닝 선형 회귀
1. 회귀
- 연속적인 실수 값을 예측하는 분야
2. 선형 회귀 (Linear Regression)
- 직선의 형태를 가지는 1차식으로 연속적인 실수 값을 예측하는 모델
- 여러 개의 독립변수 x(특성)와 종속변수 y(예측값)의 선형 상관 관계를 모델링
- 규제가 있는 회귀 모델(Lasso, Ridge)과 딥러닝 이론의 기초
- 회귀는 현업에서 많이 사용되며 활용 분야가 매우 넓음


- 선형 회귀 예시
y = wx + b
y : 종속(응답) 변수
w : 기울기(가중치)
x : 독립(입력) 변수
b : 절편(편향)


학습 데이터에는 없는 미지의 데이터에 대한 값을 예측할 때, 데이터의 분포를 가장 잘 표현할 수 있는 직선(y=wx+b)을 그려서 값을 예측

- 다중 선형 회귀 함수

- 회귀 모델의 성능 평가 : 예측값과 원데이터의 오차를 비교
MSE, RMSE, MAPE, R2 Score

① MSE, RMSE : 예측 대상의 크기에 영향을 받음
※ MSE 구하는 방법
오차의 제곱을 구한다. (오차 : 예측값에서 정답값의 차) → 구한 값의 평균을 구한다.

② MAPE

③ R2 Score

※ R2 Score가 1일 경우
모든 데이터가 선 위에 올라가 있음
④ MAE(Mean Absolute Error) : 오차의 절댓값을 구한 후 평균값
- 선형회귀 모델의 최종 목표 : MSE가 최솟값이 되는 w, b를 찾기
① 수학 공식을 이용한 해석적 방법 (Ordinary Least Squares) : 선형회귀 모델 내부에 이미 구현되어 있음
② 경사하강법(Gradient Descent Algorithm) : 기계가 스스로 학습한다는 머신, 딥러닝의 개념을 있게 한 핵심 알고리즘 - 경사하강법 : 비용함수의 기울기(경사)를 구하여 기울기가 낮은 쪽으로 계속 이동하여 값을 최적화시키는 방법
우선 임의로 w 값을 설정
① 최적 w값을 찾아가기 위해 시작점에서 손실 곡선의 기울기를 계산 → 비용함수를 w에 대해 편미분
② 파라미터를 곱한 것을 초기 설정된 w값에서 빼 줌
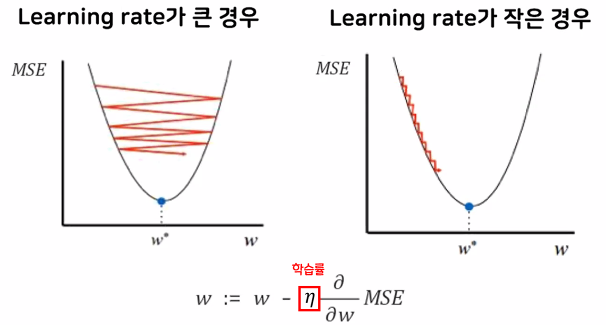
학습률(Learning rate) : 기울기의 보폭
학습률이 너무 작으면 최적 w를 찾는데 오래 걸리고, 너무 크면 건너뛰어 버릴 수 있음



- MSE 값을 최소화하는 경사하강법을 거치면서 최적의 직선을 생성

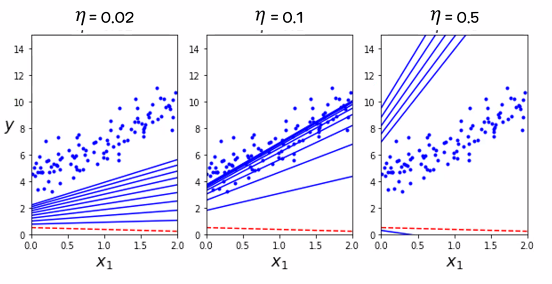
- 학습률(Learinig rate, η) 비교
최적의 학습률(정확도 + 속도)을 찾는 것이 중요
- 확률적 경사하강법(Stochastic Gradient Descent)
큰 데이터 셋에서 일반 경사하강법의 느린 단점을 보완하기 위한 방식
전체 데이터가 아닌 일부 데이터만으로 w, b 값을 업데이트
항상 좋은 방향으로만 업데이트가 일어나지는 않지만, 속도가 빠름
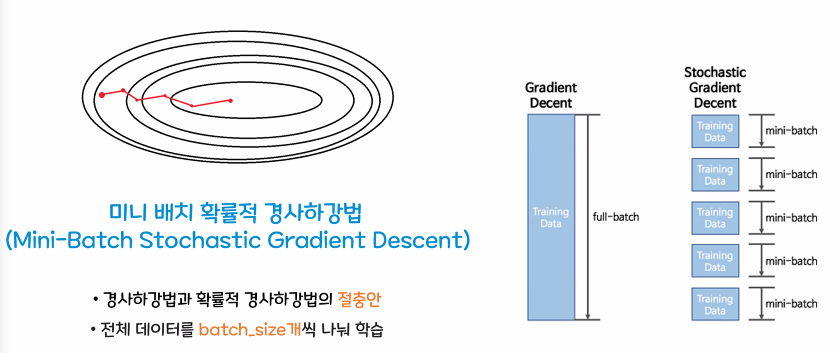
※ 경사하강법과 확률적 경사하강법 비교

- 미니 배치 확률적 경사하강법(Mini-Batch Stochastic Gradient Descent)
경사하강법과 확률적 경사하강법의 절충안
전체 데이터를 batch_size개씩 나누어서 학습
3. Lenear Model 장단점
- 장점
결과예측(추론) 속도가 빠르며, 대용량 데이터에도 충분히 활용 가능
특성이 많은 데이터 세트라면 훌륭한 성능 - 단점
특성이 적은 저차원 데이터에서는 다른 모델의 일반화 성능이 더 좋을 수 있음
4. 규제 (Regularization)
- 선형회귀 모델에서 과대적합 위험을 감소시키기 위해 w값의 비중을 줄이기
- 선형회귀 모델은 학습 데이터를 전부 반영하여 하나의 직선 방정식을 만드므로, 학습 데이터에 과대적합 되는 것을 방지 하는 방법이 없음
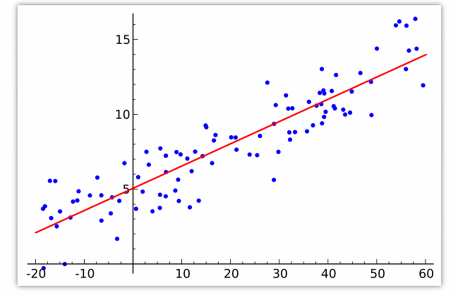
- 모델 정규화
w(회귀 계수)값이 크다 : 입력에 따른 예측 결과가 크게 바뀜, 새로운 데이터가 들어오면 제대로 예측 불가(과대적합)
→ w값을 적절히 낮게 조절하여 과대적합의 위험을 줄이는 규제가 필요
- L1 규제 : Lasso
w의 모든 원소에 똑같은 힘으로 규제를 적용
특정 계수(가중치가 낮은 원소)들은 0, 특성선택(Feature Selection)이 자동으로 일어남 - L2 규제 : Ridge
w의 모든 원소에 골고루 규제를 적용하여 0에 가깝게 만들기 (보통 Lasso보다 Ridge를 많이 사용)
| 구분 | Lasso | Ridge | ElasticNet |
| 적용 규제 | L1 | L2 | L1 + L2 |
| 특징 | 중요하지 않은 변수는 제외 특성 간 상관관계가 상대적으로 낮은 경우 사용 |
모든 변수에 같은 비율로 규제 적용 특성 간 상관관계가 상대적으로 높은 경우 사용 |
L1 규제로 변수 자체를 줄이고, L2 규제로 남은 변수들의 영향도를 줄임 특성 수가 데이터 수보다 많을 때 사용 |

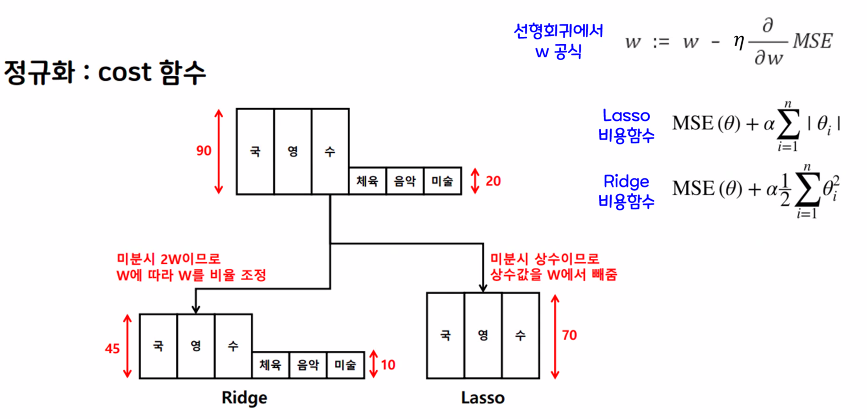
L1(Lasso), L2(Ridge) 비교

※ Kaggle 주택가격 예측을 이용해 비교

- 주요 매개변수(Hyperparameter)
alpha : 규제의 강도, Ridge(alpha), Lasso(alpha) (※scikit-learn)
alpha값이 커짐 → 규제 효과가 커짐 (과대적합 감소, 오차 증가)
alpha값이 작아짐 → 규제 효과가 작아짐 (과대적합 증가, 오차 감소)
단, alpha값이 0이되면 선형회귀와 같음
ex) alpha 값 바꾸기

'Machine Learning' 카테고리의 다른 글
| 머신러닝 로지스틱 회귀(Logistic Regression) (0) | 2023.03.24 |
|---|---|
| 머신러닝 앙상블(Ensemble) (0) | 2023.03.20 |
| 머신러닝 Decision Tree, 교차 검증, 특성 선택 (0) | 2023.03.20 |
| 머신러닝 분류 평가 지표 (0) | 2023.03.12 |
| 머신러닝 기초 3, KNN모델을 이용한 붓꽃 품종 분류 실습 (0) | 2023.03.12 |




댓글